Bài dịch google
Chúng tôi đã tương quan thứ nguyên Fractal với rủi ro đầu tư. Một mô hình đơn giản được đưa ra bởi tình huống sau. Các nhà giao dịch có kinh nghiệm tham gia thị trường, tức là có một vị thế mở sau khi có tín hiệu MUA vào trong chiến lược giao dịch của họ báo hiệu cho họ một xu hướng bắt đầu, nhìn thấy hoặc cảm thấy rủi ro ngày càng tăng, mong đợi sự kết thúc của xu hướng và bắt đầu bán. Họ bắt đầu bán sớm hơn những người khác (chưa có nhiều kinh nghiệm), những người tiếp tục mua vì họ tin rằng thị trường sẽ tiếp tục phát triển. Giá có thể tiếp tục tăng. Nhưng sau một khoảng thời gian cụ thể, ngày càng có nhiều nhà giao dịch bắt đầu bán các vị thế của họ, và các nhà giao dịch thiếu kinh nghiệm cũng bắt đầu hiểu tình hình và bắt đầu bán.Tại thời điểm này, giá bắt đầu giảm xuống.
Giả thuyết của chúng tôi là chúng tôi có thể ước tính thời điểm mà các nhà giao dịch thông minh bắt đầu bán. Có khả năng cảm giác của họ tương quan với những thay đổi về kích thước fractal. Các chỉ báo kỹ thuật tiêu chuẩn phản ứng với sự thay đổi của giá, nhưng có khả năng là việc các nhà giao dịch khôn khéo bắt đầu bán không tác động đến giá đủ mạnh để ảnh hưởng đến các chỉ báo kỹ thuật tiêu chuẩn. Chúng tôi cho rằng các thuộc tính hỗn loạn có thể phản ứng trước khi giá thay đổi. Do đó, chúng tôi mong đợi nhiều lợi nhuận hơn khi sử dụng chiến lược dựa trên những thay đổi về thứ nguyên fractal.
Ý tưởng về phương pháp phi tuyến tính của chúng tôi tương tự như cơ chế của MACD. Tuy nhiên, thay vì các
đường trung bình động được tính toán từ các giá trị hàng ngày của chuỗi thời gian trong một kích thước hộp nhất định, chúng tôi sử dụng số mũ di chuyển Hurst được tính toán từ thứ nguyên fractal của lợi nhuận hàng ngày trong một kích thước hộp nhất định.
Chúng tôi đã thử nghiệm với các kích thước hộp di chuyển khác nhau để di chuyển số mũ Hurst và với các khoảng thời gian trả về R khác nhau, tức là đối với mỗi chuỗi giá trị thời gian, chúng tôi đã xây dựng một chuỗi thời gian của lợi nhuận cho một khoảng thời gian R nhất định và tìm kiếm tối đa một hàm lợi nhuận là ba các biến - H-nhanh, H-chậm và R.
Cuối cùng, sau khi tính toán bạo lực tốn thời gian, chúng tôi đã thu được kết quả lợi nhuận tốt nhất cho số mũ Hurst chuyển động nhanh H-fast = H16 (tức là số mũ Hurst được tính trong khoảng thời gian trong 16 ngày qua), số mũ Hurst chuyển động chậm H -slow = H32 (tức là, số mũ Hurst được tính cho khoảng thời gian trong 32 ngày qua) và cho khoảng thời gian trả về là một ngày R1.
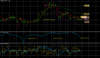
Vì vậy, chúng tôi tạo ra các tín hiệu MUA hoặc BÁN tại mỗi điểm giao nhau của H16 và H32 như trong Hình 1. Trong các công thức sau, n biểu thị chỉ số của một phần tử chuỗi thời gian.
(H16 − H32) n> 0 và (H16 − H32) n + 1 <0 = ⇒ tín hiệu MUA
(H16 − H32) n <0 và (H16 − H32) n + 1> 0 = ⇒ tín hiệu BÁN
Khi H16 cắt xuống H32 thì chúng ta tạo ra tín hiệu MUA. Chúng tôi cho rằng các thuộc tính hỗn loạn sẽ giảm đi. Khi H16 giao nhau với H32 thì chúng tôi tạo ra tín hiệu BÁN. Chúng tôi cho rằng các thuộc tính hỗn loạn sẽ tăng lên.
Tất nhiên, chúng ta có thể tưởng tượng một số lượng rất lớn các cấu trúc khác thuộc loại này bao gồm mọi sự kết hợp có thể hiểu được của số mũ Hurst và bất kỳ trong số hàng trăm chỉ báo kỹ thuật hiện có. Tuy nhiên, các thử nghiệm tốn thời gian vì số lượng kết hợp quá lớn và vì khối lượng dữ liệu đầu vào (khoảng 3.000.000 phần tử dữ liệu).